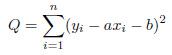 (2)
(2) 回帰分析(regression analysis)とは、因果関係が想像されるデータに対して、(多)変数間の関係式を推定し、結果用途として予測や検証に用いる統計手法をいいます。
関係式は、連続尺度の独立変数(説明変数) X
に対する従属変数(目的変数) Y
の関係として当てはまり、説明変数に対する予測値として従属変数を定量的に分析します。よって、相関が低い関係において、顕著な効果が確認できます。名義尺度を説明変数に用いる場合は、説明変数における状態と説明変数の推移を数値化して(ダミー変数の導入)解析を行います(数量化I類)。
X が1個の場合を単回帰分析、2つ以上ならば重回帰分析と呼ぶことがあります。重回帰分析では、それぞれの
X の間は無相関と仮定することが前提となります。
1次式の関係モデルを用いる場合を線形回帰、その他のモデルを用いる場合を非線形回帰と言います。
x の任意の変化に伴って y が変化するとき、x
を独立変数、 y を従属変数と言います。
今、測定によって数値の組が (x, y) = (x1,
y1), (x2, y2), (x3,
y3), … , (xn-1, yn-1),
(xn, yn) のように得られ、この関係が1次式で表わされると想定して、以下の式で近似するとします。
y' = ax + b (1)
ここで、 y' は、y の推定値を意味します。
任意の (xi, yi) について、 推定値と測定値の差は「残差(residual)」と言い e = yi' - yi で表わすことができます。y1 から yn まで残差の 2乗総和 Q は以下の式で求めることができます。
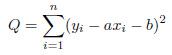 (2)
(2)
最小二乗法では、この Q が最小となるように a と b を決めていきます。式(2)は a および b の二次関数となりそうで、最小値が求められそうです。式(2)を展開します。
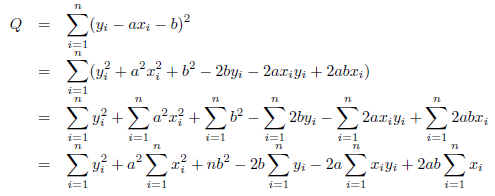 (3)
(3)
式(3)において、相和の項を、左から順にA, B, C, …に置き換えます。
Q = A + a2B + nb2 - 2bC - 2aD +2abE (4)
式(4)は、 a と b ともに2乗の項を含むので、 S が最小となるには、 a と b ともに 0 の場合です。導出を簡単にするために、式(4)を、a, b それぞれで偏微分し、それぞれを 0 と置きます。
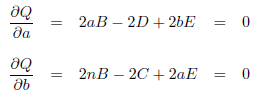 (5)
(5)
式(5)を連立方程式として解き、A, B, C, …を展開します。
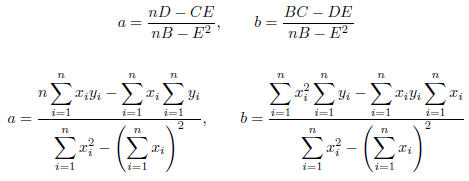 (6)
(6)
前の例では、1個の独立変数について直線を求めました。独立変数が2個になると、三次元空間の観測値を近似する平面を求めることができます。この平面を「回帰平面」と呼びます。
直線の場合と同様に、測定によって数値の組が (x, y, z) = (x1, y1, z1), (x2, y2, z2), (x3, y3, z3), … , (xn-1, yn-1, zn-1), (xn, yn, zn) のように得られ、この関係が平面で表わされると想定して、以下の式で近似するとします。
z' = ax + by + c (7)
式(7) において、独立変数は x, y です。 残差の 2乗総和 Q は以下の式で表わします。
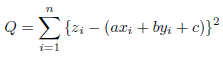 (8)
(8)
式(8)を展開し式(3)および(4)と同様に偏微分します。
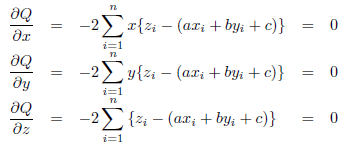 (9)
(9)
ここで、x, y, z の平均値をそれぞれ x, y, z と表す時、式(9)の三番目の式を -2n で割ることによって、定数項 c について次の関係が成り立ちます。
c = z - ax - by (10)
これを式(9)の残りの式に代入して c を消去し、整理することによって、次の連立方程式を導くことができます。
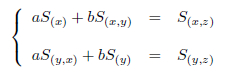 (11)
(11)
式(11)を「正規方程式」と言います。ここで、S(x) は、x の分散であり、S(x, y) は、x と y の共分散です(他の記号についても同様です)。これを解くことによって、残りの係数(偏回帰係数) x, y が導かれます。
2008/08/01: 作成